导言
光作为一种重要的信息载体和能量形式,其特性与行为的研究一直是光学领域的核心内容。涡旋光是一种具有独特螺旋相位结构和轨道角动量的特殊光束,与传统的平面波或高斯光束不同,其波前呈现螺旋状,相位分布围绕光束中心具有2π的整数倍变化,这使得每个光子携带了与拓扑电荷数相关的轨道角动量。这种独特的性质赋予了涡旋光在众多领域(光通信、光学成像、光学操纵、量子光学、激光加工、光存储等领域)潜在的应用价值。研究涡旋光的衍射特性,不仅有助于深入理解涡旋光的基本物理性质,揭示其在传播过程中的行为规律,还能为上述应用提供坚实的理论基础,推动相关技术的发展和创新。通过对涡旋光衍射的研究,可以优化涡旋光的产生、传输和检测方法,提高其在实际应用中的性能和效率,从而为解决实际问题提供更有效的光学工具和技术方案。
摘要
本文就基于衍射图样的拓扑电荷数测量方法进行了理论分析、数值模拟和实验验证。在理论分析方面,基于惠更斯-菲涅尔原理和标量衍射理论,建立涡旋光衍射的数学模型,推导涡旋光在不同衍射条件下的光场分布表达式,结合数值模拟,利用 MATLAB软件平台,编写相应的程序对涡旋光衍射过程进行模拟仿真。通过数值模拟,可以直观地展示涡旋光在不同参数条件下的衍射光场分布情况,深入分析各种因素对衍射特性的影响,为实验研究提供指导和补充。在实验研究方面,搭建涡旋光产生与衍射实验平台,利用空间光调制器、螺旋相位板等光学元件产生不同拓扑电荷数的涡旋光,并通过设置不同的衍射障碍物或孔径,观察和记录涡旋光的衍射图样。采用 CCD 相机、光电探测器等设备对衍射光场进行测量和分析,获取实验数据,验证理论分析和数值仿真的正确性。
涡旋光衍射理论分析
基于惠更斯 - 菲涅尔原理和标量衍射理论,可对涡旋光的衍射特性进行深入的理论分析。假设涡旋光的初始电场分布为[数学公式],在柱坐标系下,其表达式可写为:
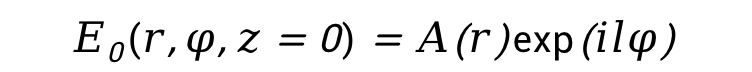
其中, 是振幅函数,描述了涡旋光在径向的振幅分布,l为拓扑荷数,
是振幅函数,描述了涡旋光在径向的振幅分布,l为拓扑荷数, 是方位角。
是方位角。
当涡旋光遇到衍射障碍物或通过衍射孔径时,根据惠更斯 - 菲涅尔原理,波面上的每一点都可看作是新的子波源,这些子波源发出的子波在空间中相互干涉、叠加,从而形成衍射光场。对于菲涅尔衍射,在距离衍射屏z处的光场分布 可通过菲涅尔衍射积分公式计算:
可通过菲涅尔衍射积分公式计算:
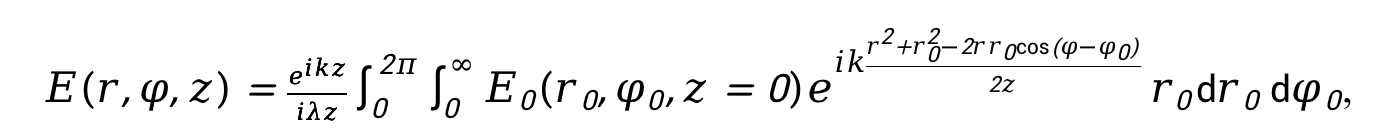
其中, 为波数,
为波数, 是光的波长,
是光的波长, 是衍射屏上的坐标,
是衍射屏上的坐标, 是观察平面上的坐标。
是观察平面上的坐标。
在夫琅禾费衍射条件下,当接收屏和衍射屏的距离足够远时,衍射光场的分布可通过夫琅和费衍射衍射积分公式简化计算:
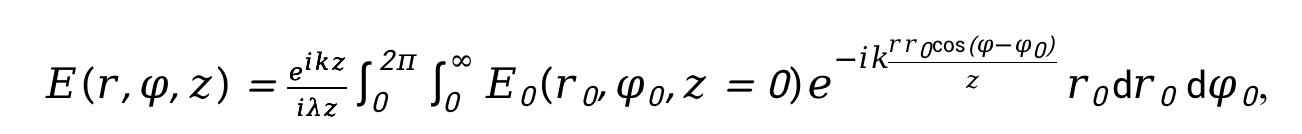
在衍射过程中,涡旋光的相位和强度会发生显著变化。由于涡旋光本身具有螺旋相位结构 ,在衍射时,这种相位结构会与衍射引起的相位变化相互作用。对于相位变化,衍射会导致相位的重新分布,使得涡旋光的螺旋相位在空间中的分布发生改变,从而影响其波前的形状和传播方向。而在强度方面,衍射会使涡旋光的光强分布发生变化,原本的环形光强分布在衍射后可能会出现旁瓣、暗纹等复杂结构,光强的最大值和最小值的位置也会发生改变。通过对上述衍射积分公式的分析和计算,可以深入了解涡旋光在衍射过程中相位和强度的具体变化规律,为进一步研究涡旋光的衍射特性提供理论基础。
,在衍射时,这种相位结构会与衍射引起的相位变化相互作用。对于相位变化,衍射会导致相位的重新分布,使得涡旋光的螺旋相位在空间中的分布发生改变,从而影响其波前的形状和传播方向。而在强度方面,衍射会使涡旋光的光强分布发生变化,原本的环形光强分布在衍射后可能会出现旁瓣、暗纹等复杂结构,光强的最大值和最小值的位置也会发生改变。通过对上述衍射积分公式的分析和计算,可以深入了解涡旋光在衍射过程中相位和强度的具体变化规律,为进一步研究涡旋光的衍射特性提供理论基础。
涡旋光经过不同光阑的衍射计算模型
假设涡旋光经过一个特殊形状的光阑(三角形、星形、方形、太极形等),光阑放置在处为初始光场平面,假设光阑可用数学形式 表示,则此时涡旋光经过此光阑后在观察面z处的光场分布可以用衍射积分公式进行计算:
表示,则此时涡旋光经过此光阑后在观察面z处的光场分布可以用衍射积分公式进行计算:
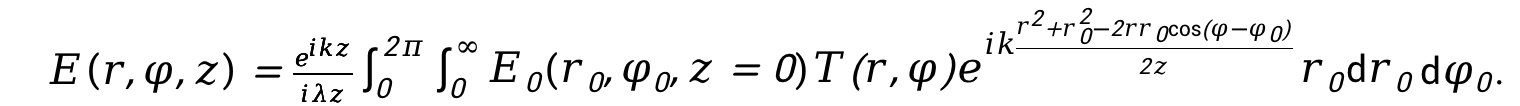
衍射孔径的形状对涡旋光的衍射图样有着显著影响。不同形状的衍射孔径会导致不同的衍射图样特征。
数值仿真理论基础
理论上可以用衍射积分公式进行直接积分或者进行直接的数值计算,但是在实际数值仿真计算中,我们可以将衍射积分公式进行改写,其在直角坐标系下可以写为
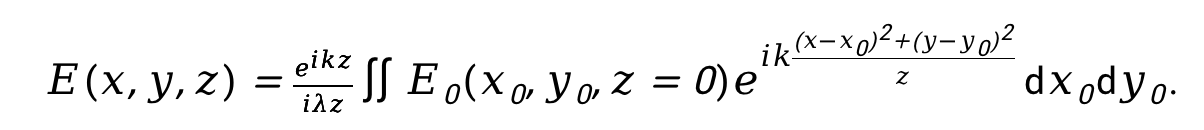
将上式中积分内的指数项展开,得
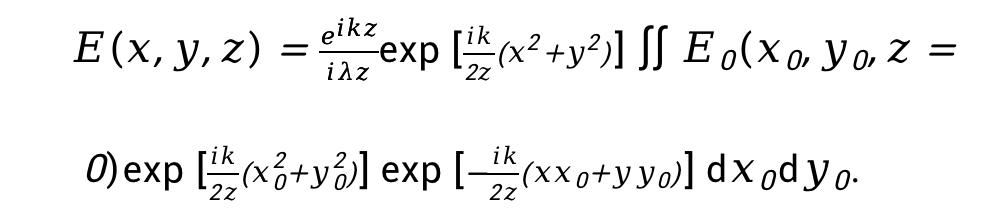
定义脉冲响应:
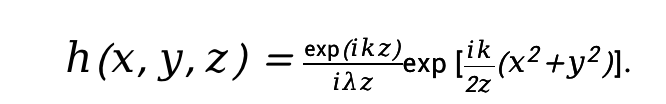
令初始光场为 ,则观察面z处的光场复振幅分布为
,则观察面z处的光场复振幅分布为
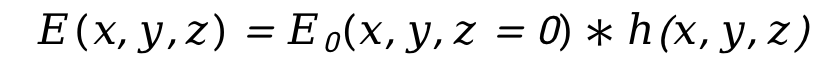
式中,* 表示卷积。由卷积定理可得
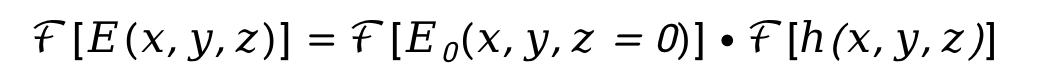
对脉冲响应进行傅里叶变换,得到菲涅尔传递函数 如下
如下
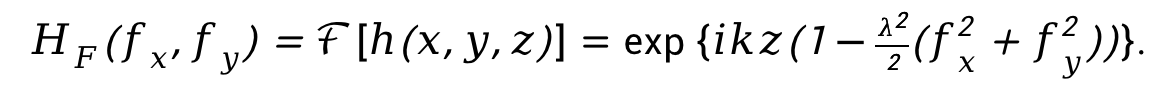
因此,观察面z处的光场可改写为
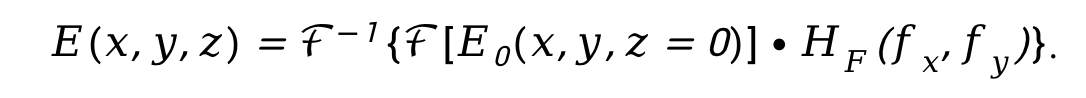
由此得到了新的衍射计算形式,通过计算初始平面光场的频谱,而后乘以传递函数得到观察面的频谱,最后进行傅里叶逆变换得到观察面的光场。而上述计算形式结合MATLAB软件平台中的fft2和ifft2函数可以非常快速的进行数值仿真计算。
涡旋光束经过不同光阑后的数值仿真结果
利用写好的MATLAB代码我们仿真了四种异形光阑,其形状分别为正三角形、星形、方形和太极形,其示意图如下图1所示。

图1:四种异形光阑示意图。
利用MATLAB得到高斯涡旋光束,然后将其经过利用不同分布函数产生相应的异形光阑,利用衍射数值计算算法,得到涡旋光束经过不同光阑后在观察平面的光强分布图。

图2:涡旋光经过不同光阑后的衍射图样。实际对应的物理尺寸为1cm*1cm。
如图2,下面一行分别示意等边三角形、五角星、矩形和太极孔光阑。上面一行则是涡旋光经过光阑后对应的衍射图案。值得注意的是,三角孔衍射的结果能够被应用于涡旋光的检测,不仅可以检测出涡旋光的拓扑荷,并且其朝向还可以很方便地得到涡旋光拓扑荷的正负。
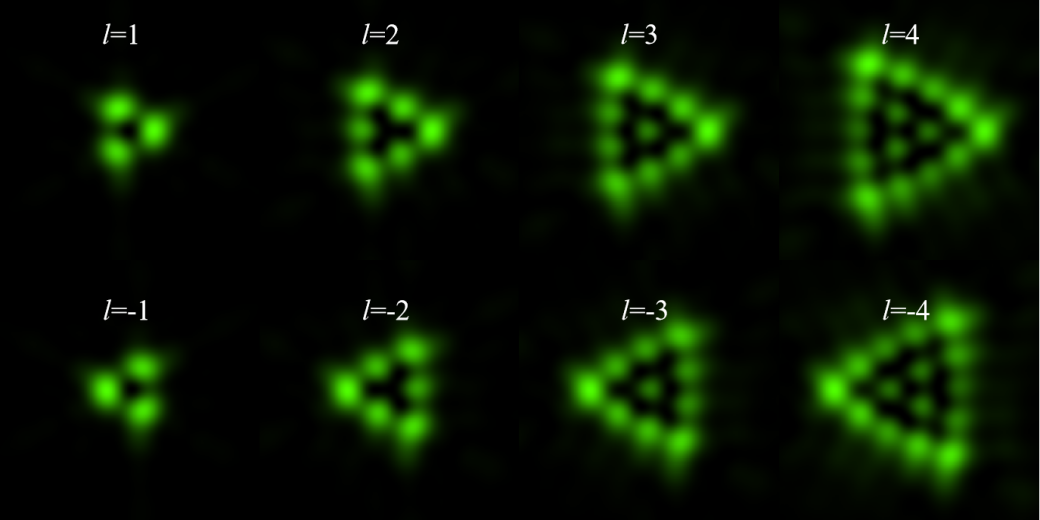
图3:不同拓扑荷涡旋光经过三角形光阑后的衍射图样。
如图3所示,当涡旋光经过三角形光阑衍射后,一条边上的散斑数目恰好等于拓扑荷数加1,并且三角形衍射图样的朝向与拓扑荷的正负负号有关。同样的我们可以分别计算出涡旋光经过星形光阑、方形光阑以及太极光阑之后的衍射图样,分别如图4、图5、图6所示。

图4:不同拓扑荷涡旋光经过星形光阑后的衍射图样。

图5:不同拓扑荷涡旋光经过方形光阑后的衍射图样。

图6:不同拓扑荷涡旋光经过太极光阑后的衍射图样。
可以看到,涡旋光束经过不同的异形光阑后其衍射图样都各不相同,其衍射图样也能与拓扑荷数及其符号相关联,具体的对应规律没有如三角形光阑的明显,但是通过图像视觉的方法可以得到对应的关系。
我们利用衍射计算程序可以计算出在不同平面的衍射图样,从而揭示出这些衍射图样的形成过程,图7演示的是涡旋光经过三角形光阑后的衍射图样的形成过程。

图7:涡旋光经过三角形光阑后的孔衍射图样的演化过程
改变衍射屏的形状,我们同样可以模拟其他形状孔径的衍射图样。图8展示了涡旋光经过星形光阑衍射图样的形成过程。

图8:涡旋光经过星形光阑后的孔衍射图样的演化过程
继续改变衍射屏的形状,可以模拟涡旋光经过方形光阑的衍射图样,图9展示了涡旋光经过方形孔径衍射图样的形成过程。
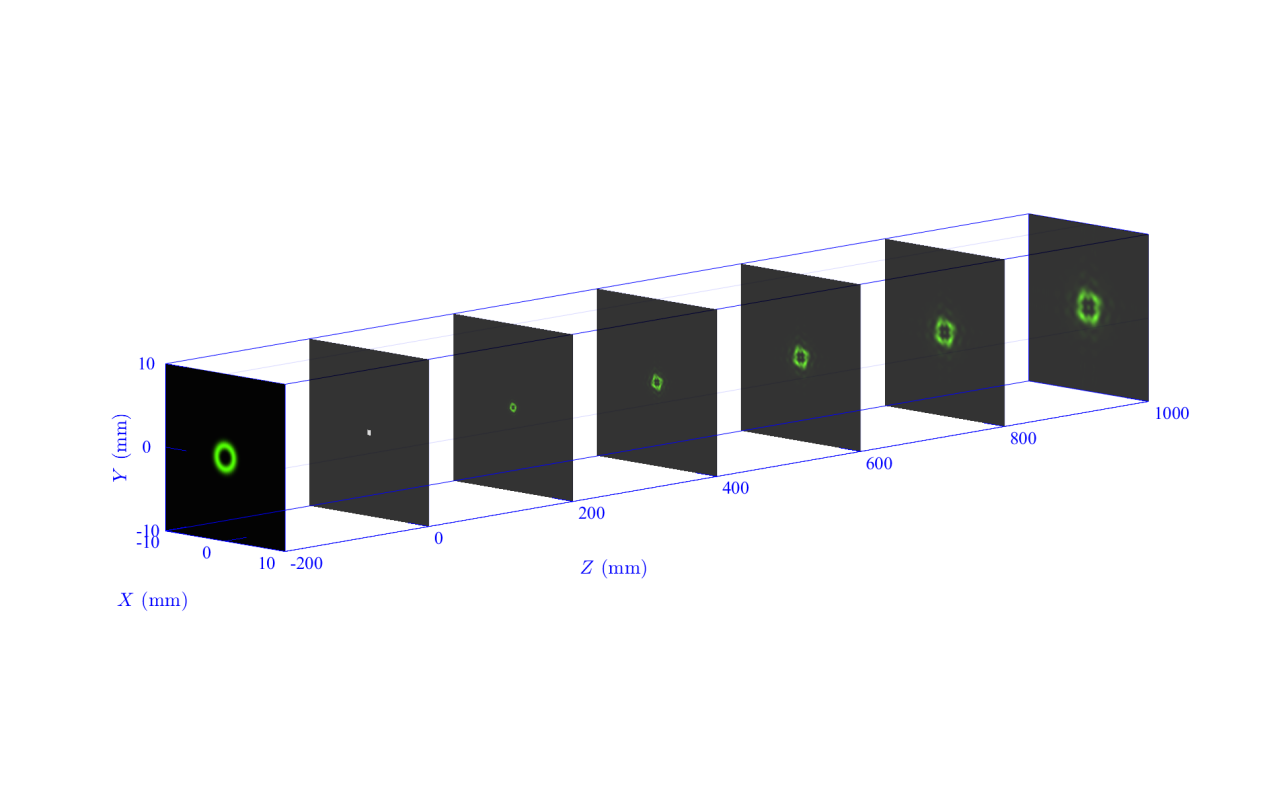
图9:涡旋光经过方形光阑后的孔衍射图样的形成过程
同样的,图10展示了涡旋光经过太极光阑孔径衍射图样的演化过程。

图10:涡旋光经过太极光阑后的孔衍射图样的演化过程
涡旋光束经过不同光阑后的实验实现和结果展示
上面展示的都是理论仿真得到的数据,那么在实验中真实的情况又是如何呢?我们将结合UPOLabs的液晶空间光调制器HDSLM80R Plus来开展实验验证。
由于HDSLM80R Plus是相位型空间光调制器(SLM),首先我们需要设法利用相位型器件实现振幅型器件的等效方法,闪耀光栅法是一种十分有效的方案,通过将异形光阑数学表达式与闪耀光栅进行相乘操作,可以很容易地实现相位型器件转换为振幅型器件使用。同时我们将涡旋相位也结合在其中,这样涡旋光的产生就不需要引入额外的调制器件。实验光路示意图如图11所示。具体操作后加载到SLM的图片如图12-图15所示。
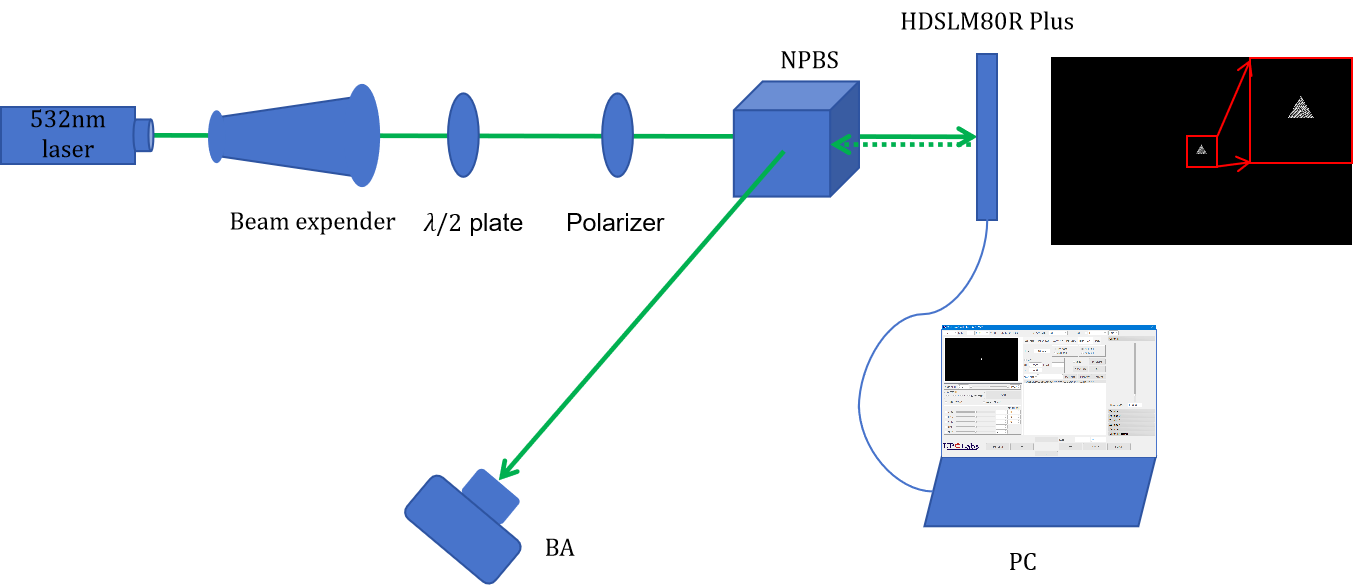
图11 实验光路示意图。BA:光斑分析仪;PC:笔记本电脑。

图12:涡旋光三角形光阑衍射SLM加载图像示意图
(涡旋光拓扑荷为4的图例)
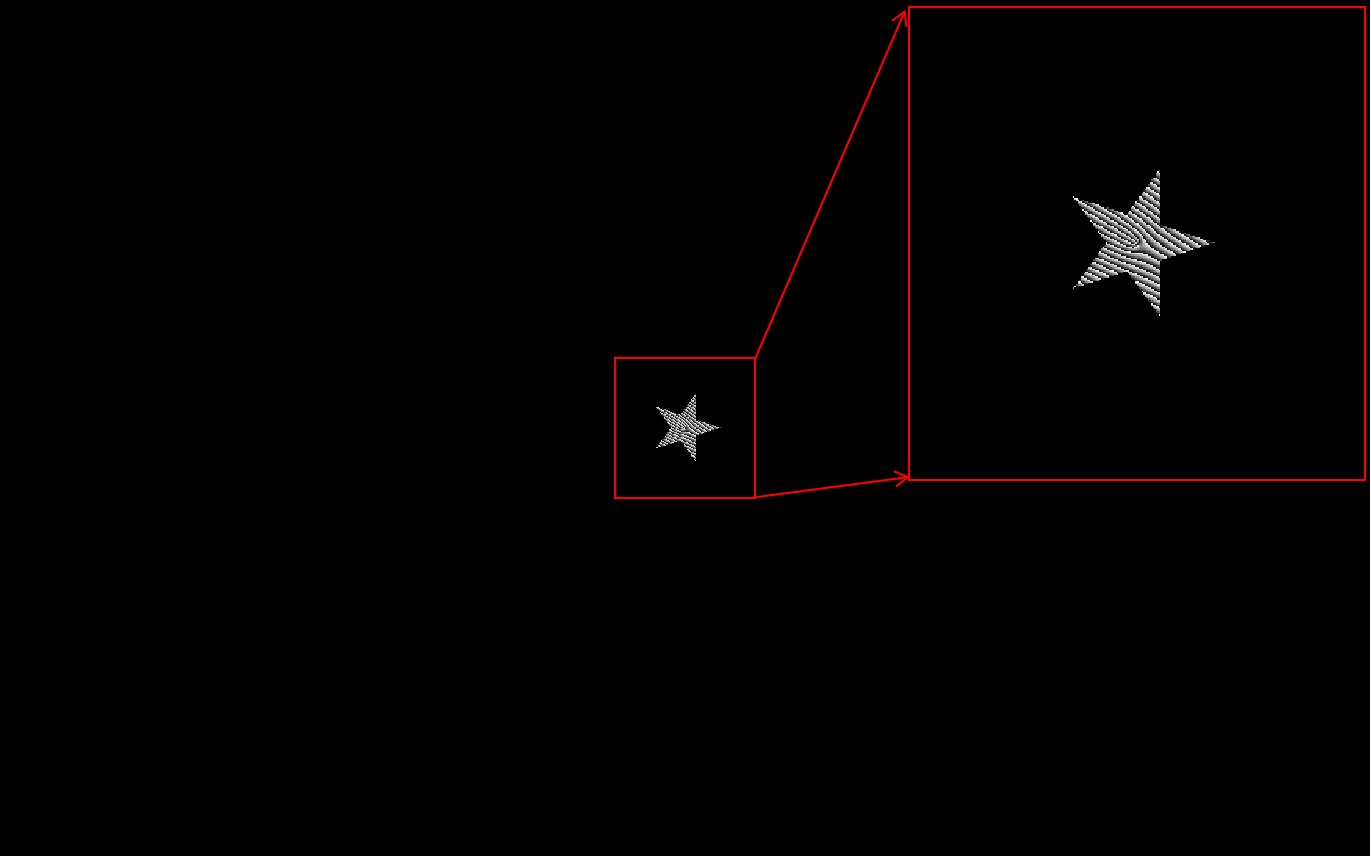
图13:涡旋光星形光阑衍射SLM加载图像示意图
(涡旋光拓扑荷为4的图例)

图14:涡旋光方形光阑衍射SLM加载图像示意图
(涡旋光拓扑荷为4的图例)
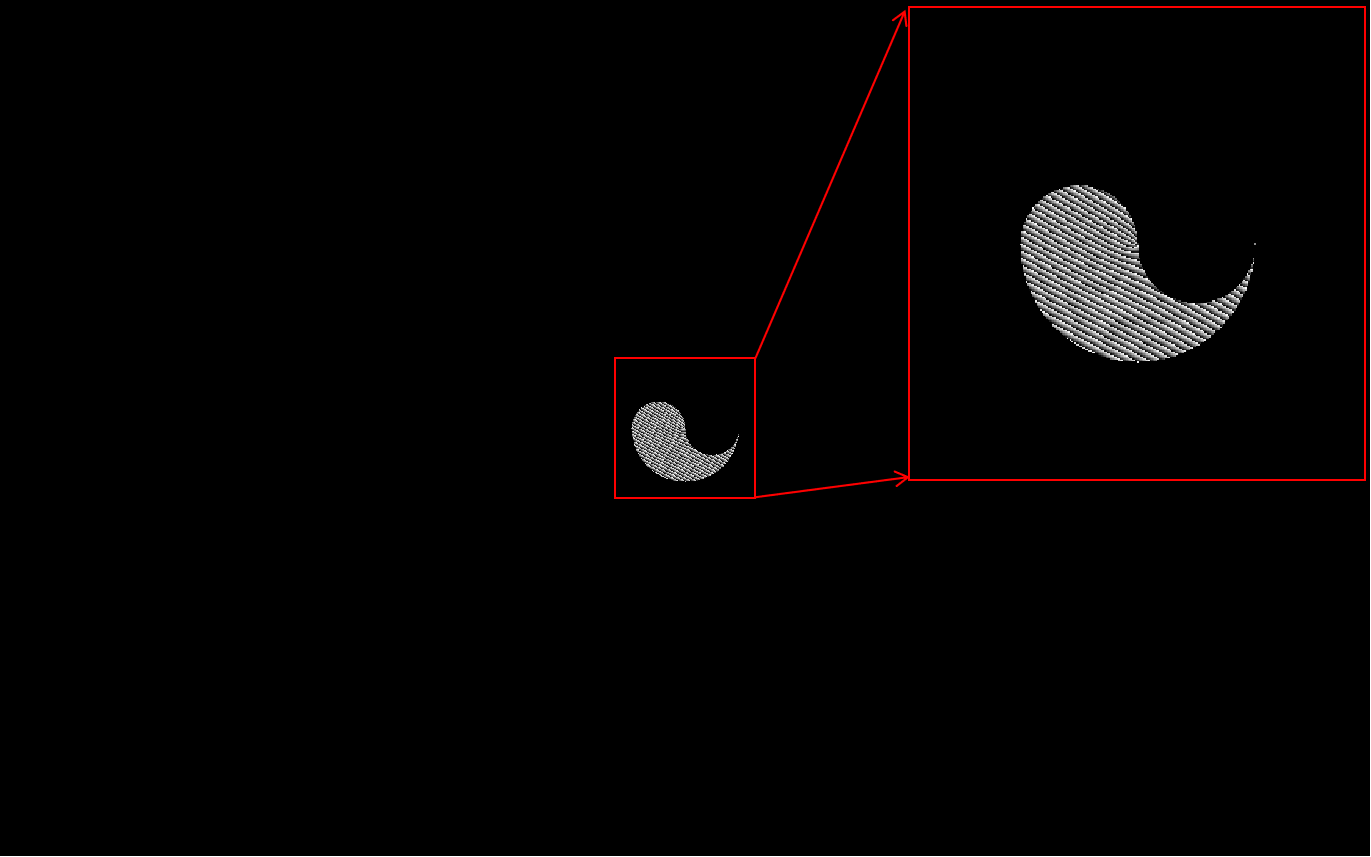
图15:涡旋太极形光阑衍射SLM加载图像示意图
(涡旋光拓扑荷为4的图例)
具体的衍射实验结果如图16-图19所示,图中的实际物理尺寸均为1cm*1cm。可以发现实验结果通理论仿真结果十分吻合。这表明理论仿真结合SLM实验研究涡旋光束的衍射特性是一套切实可行的研究方法,相信该研究范式在其他光场传输研究中也能发挥其效果。

图16:不同拓扑荷涡旋光经过三角形光阑后的衍射图样实验结果。
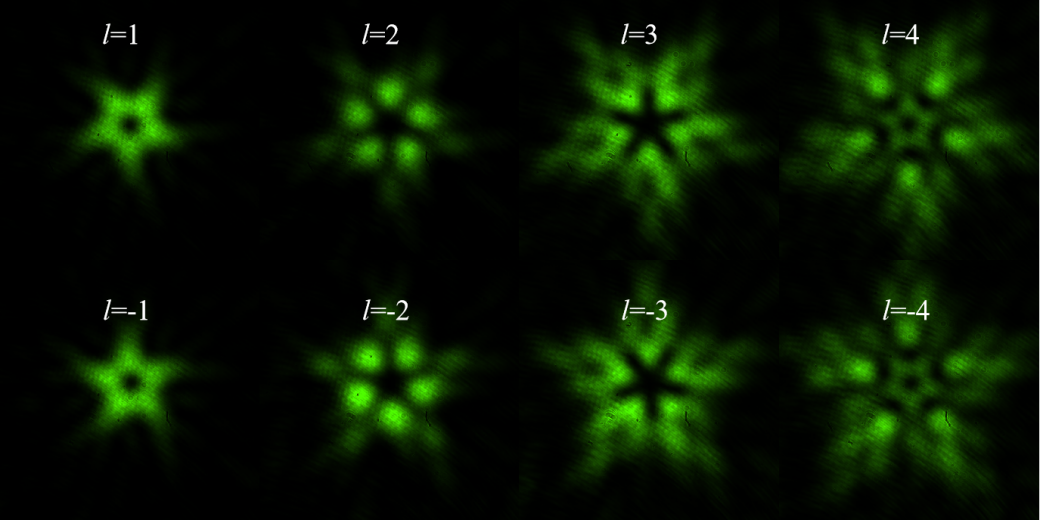
图17:不同拓扑荷涡旋光经过星形光阑后的衍射图样实验结果。

图18:不同拓扑荷涡旋光经过方形光阑后的衍射图样实验结果。
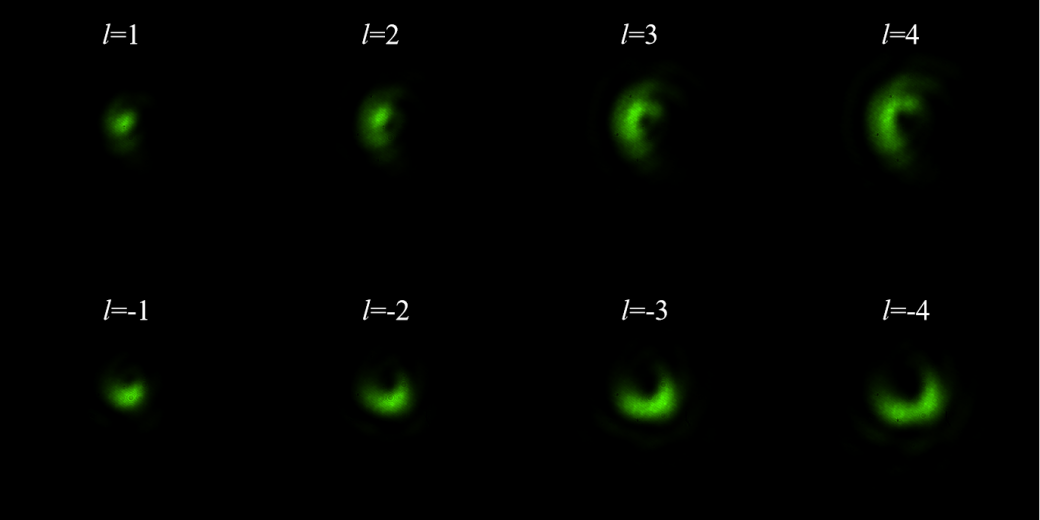
图19:不同拓扑荷涡旋光经过太极光阑后的衍射图样。
参考文献
[1] 1. W. Goodman, Introduction to Fourier Optics. New York, NY, USA:McGraw-Hill2005.
[2] C. Rosales-Guzmán and A. Forbes, How to Shape Light With Spatial Light.Modulators. Bellingham, WA, USA: SPIE,2017.
[3] Shen D, Wang K, Zhao D. Generation and propagation of a new kind of power-exponent-phase vortex beam[J]. Optics express, 2019, 27(17): 24642-24653.