导读

4-f系统是一种经典的光学系统，广泛应用于傅里叶变换光学、图像处理、光学信息处理和全息术等领域^[1]。4-f系统利用两个透镜和光学傅里叶变换的特性，实现空间频率的调制和分析。

一、4-f系统的基本原理

4-f系统的名称来源于其结构，若L1的焦距f₁与L2的焦距f₂相等，此时整个系统的距离为4f，此时为标准的4-f系统，像面和物面的光场区域是1:1的比例。如果L1和L2的焦距不同，此时除了相比于标准的4-f系统在像面的光场大小（像面水平以及竖直方向）缩放比例为f₂:f₁，其他作用和标准的4-f系统一致。

图1 4-f系统示意图

其基本结构如下：

1. 输入面：放置待处理的光学信息（如图像或光束）。

2. 第一透镜：焦距为 f₁，对输入面的光场分布进行傅里叶变换。

3. 傅里叶面：位于第一透镜的焦平面处，形成输入光场的傅里叶变换。在傅里叶面处可以放置光学滤波器，进行频域调制。

4. 第二透镜：焦距为f₂，将傅里叶变换后的光场进行傅里叶变换，恢复到空间域。

5. 输出面：位于第二透镜的焦平面处，显示处理后的光学信息。

在4f系统中，输入光场U(x,y) 经过第一透镜后，在傅里叶面上形成其傅里叶变换。傅里叶面上的光学滤波器可以对特定的空间频率成分进行调制。经过第二透镜后，傅里叶面上的调制光场再次进行傅里叶变换，形成输出光场U^’(x,y)。

这个过程可以用数学公式表示为：

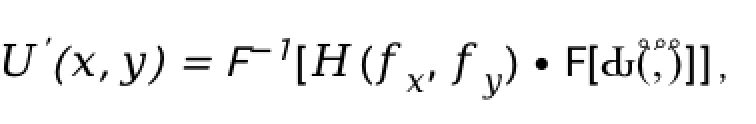
其中，表示傅里叶变换，表示傅里叶逆变换，是傅里叶面上的滤波器函数。

二、4-f系统在空间光调制器光路中的应用

如果在图1中的物面处放置一个空间光调制器，在傅里叶面处放置一个可调光阑，利用光阑滤出在傅里叶面处合适的衍射级次（通常设置为1级衍射级次），在像面可以实现非调制光（零级光、前表面反射光）的干扰减弱或者实现一些复杂的复振幅光场调控。另外，如果产生的光场是在SLM面的较近距离处，由于空间上的考虑，通常不可能将探测器离SLM足够近，此时就可以利用4-f系统实现光场中继的作用，此时的像面对应光场调控的初始平面^[2]。整个系统的光路图如下图所示。

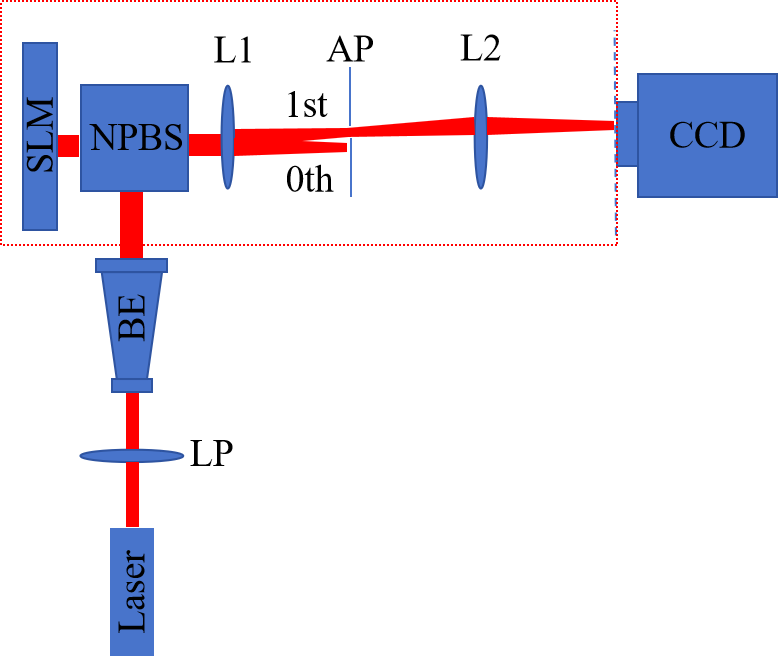
图2 空间光调制器结合4-f系统光路图。

Laser：激光器；LP：偏振片；BE：扩束镜；SLM：空间光调制器；L1，L2：透镜；AP：光阑；CCD：相机。

应用1 叠加闪耀光栅相位去除0级光影响

空间光调制器由于调控的液晶区域呈现周期性的像素分布，入射激光打到周期性结构上会发生类晶格散射现象，从而会在0级区域产生不可被调控的光分量，此时若对调制的相位图叠加一个闪耀光栅相位（线性相位），则可以用来消除0级光的影响。我们以涡旋光为例，观察叠加闪耀光栅相位利用4-f系统滤波后在像面后26cm的调制效果和自由传播26cm的调制效果，可以发现利用4-f系统滤波后产生得到的涡旋光相比直接产生的涡旋光效果会更好。此应用案例实验结果利用UPOLabs HDSLM45R得到。

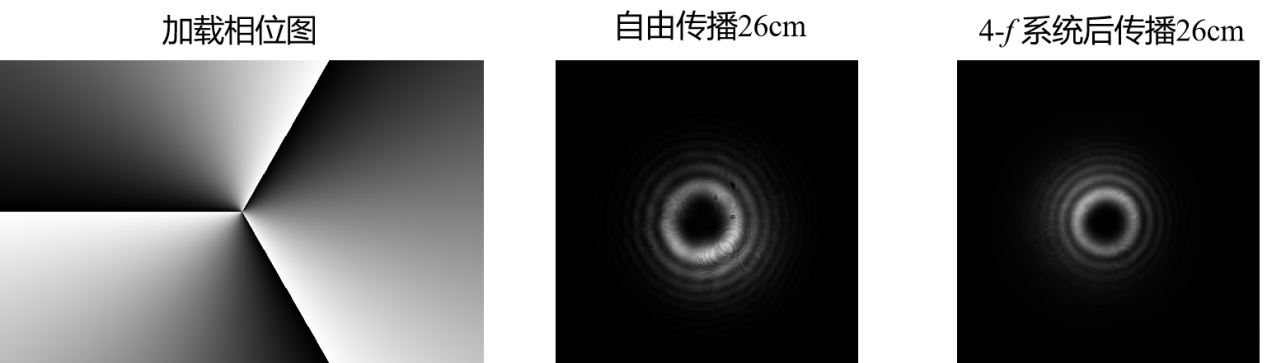
图3 自由空间和利用4-f系统滤波后的涡旋光传输26cm的光强比较结果。

应用2 复振幅光场调控

使用空间光调制实现高阶厄米-高斯光束和高阶拉盖尔-高斯光束，此时需要结合4-f系统对入射高斯光进行复振幅光场调控，进而在像面得到相应的光场分布。此应用案例实验结果利用UPOLabs HDSLM80R得到。

图4 利用4-f系统产生高阶厄米-高斯光束和拉盖尔-高斯光束[3]。

(a)(b)加载在空间光调制器上的的相位图；（c）对应的光场强度分布。

应用3 涡旋阵列调控

利用全息方法产生涡旋阵列，若涡旋光束阵列相邻涡旋光束间距较大，则激光经过加载相应相位图的SLM后自由传输一定距离可以在相应平面观察到涡旋阵列。若涡旋光束排列非常紧密，相互之间的间距如果非常小，此时激光经过加载相应相位图自由空间传输在某一平面得到的涡旋阵列相邻之间的涡旋光束是相互干扰的，无法得到想要的实验效果。此时利用4-f系统在傅里叶面处对一级衍射级次进行空间滤波，则可以在像面附近得到理想效果的涡旋阵列。实验加载的相位图和实验效果图如图5所示。

图5 利用4-f系统产生涡旋光束阵列

另外，在此实验中，若CCD相机摆放的位置位于L2和像面之间，且离L2较近或者距离4-f系统像面后方较远，此时产生的小间距涡旋阵列相邻涡旋会存在相互干涉的情况，本实验中设置的4-f系统中透镜L1和L2的焦距f₁=f₂=150mm。观察距离像面不同距离处涡旋阵列的强度分布情况，实验结果如图6所示。因此在实验中若发现产生的涡旋阵列不理想，可以考虑CCD相机观察面的位置选择是否有问题，或者考虑透镜的焦距是否与实际的焦距有所出入导致。此应用案例实验结果利用UPOLabs HDSLM38R得到。

图6利用4-f系统产生涡旋光束阵列在像面前后的成像情况。

（a）小间距涡旋阵列；（b）大间距涡旋阵列。

参考文献

[1] J. W. Goodman, Introduction to Fourier Optics. New York, NY, USA:McGraw-Hill, 2005.

[2] C. Rosales-Guzmán and A. Forbes, How to Shape Light With Spatial Light. Modulators. Bellingham, WA, USA: SPIE, 2017.

[3] Shen, Donghui, et al. "Mode conversion and transfer of orbital angular momentum between Hermite-Gaussian and Laguerre-Gaussian beams." IEEE Photonics Journal 14.1 (2022): 1-6.